Let $A: \mathbb{R}^{p} \rightarrow \mathbb{R}^{n}$ and $y \in \mathbb{R}^{p}$. Consider the following regularization problem:
\[\newcommand{\norm}[1]{\left\lVert#1\right\rVert} \begin{equation} \min_{x \in \mathbb{R}^{n}} \frac{1}{2} \norm{Ax - y}_{2}^{2} + \alpha \norm{x}_{1}. \label{eq:min-problem} \end{equation}\]This type of penalized regression is known as Lasso, see Tibshirani’s original paper (Tibshirani, 1996). It belongs to a more general type of regularization known as Tikhonov regularization (Tikhonov & Arsenin, 1977).
In this post, we first derive the dual problem, then show that the solution $x^{*}$ can be determined with the help of a projection operator. Under the assumption that $A^{-1}$ exists, the solution $x^{*}$ can be further expressed in terms of a mapping $\left(A^{T}\right)^{-1}$ from the dual space as a function of $y$. This is illustrated in Figure 1.
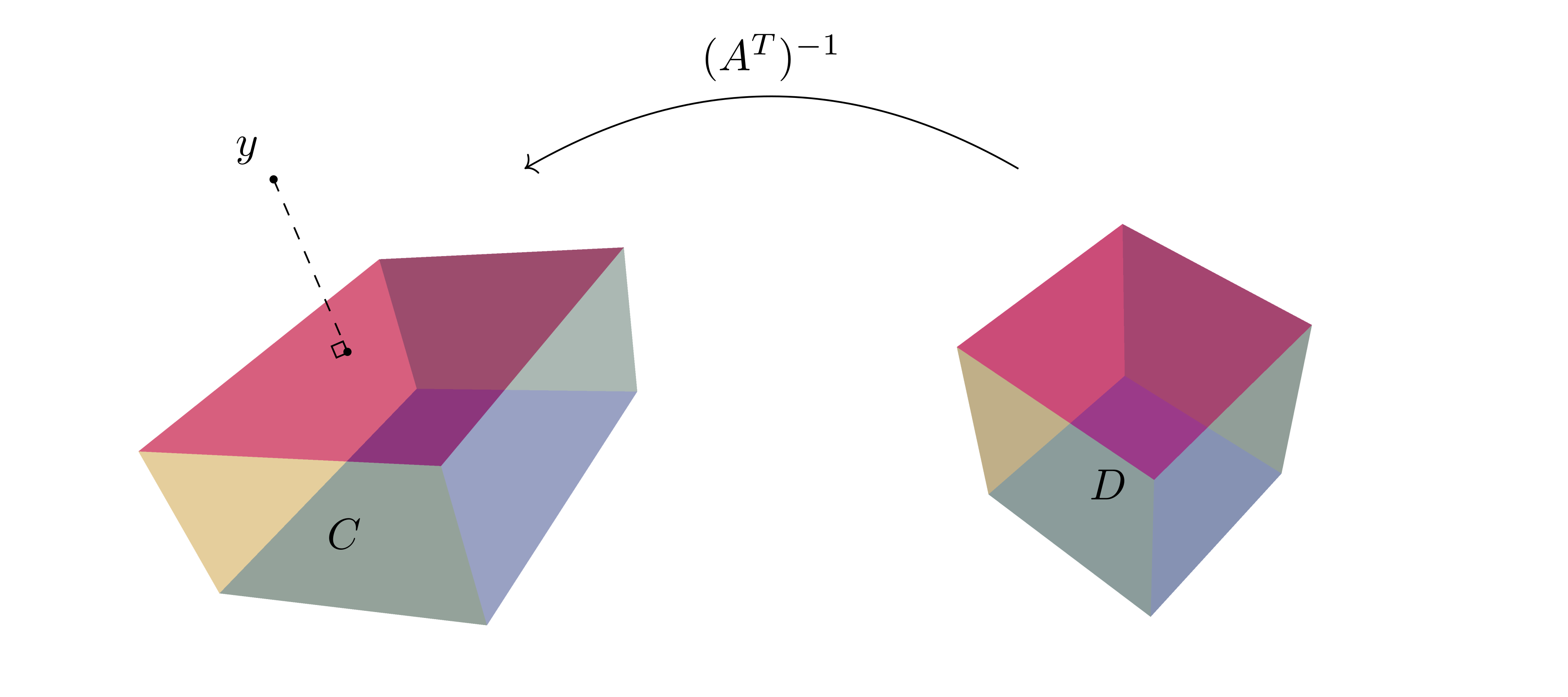
Table of contents
- Formulation of the dual problem
- Solution of the dual problem
- Solution of the primal problem
- References
Formulation of the dual problem
To derive the dual problem, introduce a dummy variable $z \in \mathbb{R}^{n}$
\[z = Ax\]and reformulate the minimization problem in \eqref{eq:min-problem} as a constrained problem P:
\[\begin{align*} \label{eq:primal-problem} \tag{P} &\underset{z \in \mathbb{R}^{n}, \, x \in \mathbb{R}^{p}}{\text{minimize}} \quad \frac{1}{2} \norm{y - z}_{2}^{2} + \alpha \norm{x}_{1} \\ &\text{subject to } \quad z = Ax \end{align*}\]Then, construct the Lagrangian by introducing the dual variable $p \in \mathbb{R}^{n}$, containing $n$ Lagrange multipliers:
\[L(x, z, p) = \frac{1}{2} \norm{y - z}_{2}^{2} + \alpha \norm{x}_{1} + p^{T} (z - Ax).\]The dual objective function is:
\[g(p) = \min_{z \in \mathbb{R}^{n}, \, x \in \mathbb{R}^{p}} \left\lbrace \frac{1}{2} \norm{y - z}_{2}^{2} + \alpha \norm{x}_{1} + p^{T} (z - Ax) \right\rbrace\]We will split the terms depending on $z$ and $x$ and minimize each part separately:
\[\begin{align*} g(p) &= \min_{z \in \mathbb{R}^{n}, \, x \in \mathbb{R}^{p}} \left\lbrace \frac{1}{2} \norm{y}_{2}^{2} - y^{T}z + \frac{1}{2} \norm{z}_{2}^{2} + p^{T}z + \alpha \norm{x}_{1} - p^{T}Ax \right\rbrace \\[.5em] &= \min_{z \in \mathbb{R}^{n}} \left\lbrace \frac{1}{2} \norm{y}_{2}^{2} - (y - p)^{T}z + \frac{1}{2} \norm{z}_{2}^{2} \right\rbrace + \max_{x \in \mathbb{R}^{p}} \left\lbrace \alpha \norm{x}_{1} - (A^{T}p)^{T}x \right\rbrace \end{align*}\]The stationarity condition says that at the optimal point, the subgradient of $L(x, z, p)$ with respect to $x$ and $z$ must contain 0. For the first part, since $L(x, z, p)$ is differentiable in $z$, the subgradient with respect to $z$ equals the gradient. By taking $\frac{\partial}{\partial z} L(x, z, p)$ and setting it to $0$, we get the stationarity condition:
\[z = y - p^{*}\]Plugging this into the first part, yields:
\[\frac{1}{2}\norm{y}_{2}^{2} - (y - p^{*})^{T}(y - p^{*}) + \frac{1}{2}\norm{y - p^{*}}_{2}^{2} = \frac{1}{2}\norm{y}_{2}^{2} - \frac{1}{2}\norm{y - p^{*}}_{2}^{2}.\]For the second part, because $\alpha \norm{x}_1$ is a non-differentiable function of $x$, we need to compute the subdifferential $\partial (\alpha \norm{x}_1)$.
From the rules for the subgradient, see (Boyd & Vandenberghe, 2008), we can derive that the $\partial \norm{x}_{1}$ can be expressed as follows:
\[\partial (\norm{x}_{1}) = \lbrace g : \norm{g}_{\infty} \leq 1, g^{T} x = \norm{x}_{1} \rbrace.\]Furthermore, by using the rule for scalar multiplication:
\[\partial (\alpha\norm{x}_{1}) = \lbrace g : \norm{g}_{\infty} \leq \alpha, g^{T} x = \alpha\norm{x}_{1} \rbrace\]we get the following stationarity condition:
\[g = A^{T}p \in \partial \alpha \norm{x}_{1}\]when
\[\begin{align*} \norm{A^{T}p}_{\infty} &\leq \alpha \\[.5em] \alpha \norm{x}_{1} &= (A^{T}p)^{T}x. \end{align*}\]Therefore, the dual problem D is:
\[\begin{align*} \label{eq:dual-problem} \tag{D} &\max_{p \in \mathbb{R}^{n} } \, \frac{1}{2}\norm{y}_{2}^{2} - \frac{1}{2}\norm{y - p}_{2}^{2} \\[.5em] &\text{subject to } \, \norm{A^{T}p}_{\infty} \leq \alpha \end{align*}\]Solution of the dual problem
The solution $p^{*}$ of the dual problem will be determined with the help of a projection operator. Looking at the dual problem formulation \eqref{eq:dual-problem}, we see that $\frac{1}{2}\norm{y}_{2}^{2}$ can be omitted, since it doesn’t depend on $p$. Then, multiplying it by 2 and reversing the sign, we arive at equivalent dual problem:
\[\begin{align*} \label{eq:dual-problem-prime} \tag{D'} &\min_{p \in \mathbb{R}^{n} } \, \norm{y - p}_{2}^{2} \\[.5em] &\text{subject to } \, \norm{A^{T}p}_{\infty} \leq \alpha. \end{align*}\]Let $C \subset \mathbb{R}^{n}$ be closed and convex set. Define a projection operator $P_{C}$ as:
\[\DeclareMathOperator*{\argmin}{arg\,min} \begin{align*} P_{C} \text{: } & \mathbb{R}^{n} \rightarrow C \\[.5em] & y \mapsto P_{C}(y) := \argmin_{p \in C} \norm{y - p}_{2}. \end{align*}\]Looking at \eqref{eq:dual-problem-prime}, we see that $p^{*}$ is a projection
\[p^{*} = P_{C}(y)\]where $C$ is equal to:
\[C = \lbrace p \in \mathbb{R}^{n} : \norm{A^{T}p}_{\infty} \leq \alpha \rbrace.\]Notice that $C$ is indeed closed and convex. It can be expressed as:
\[\begin{equation}\nonumber C = (A^{T})^{-1}(D) \end{equation}\]where $D$ is equal to:
\[D = \lbrace d \in \mathbb{R}^{p} : \norm{d}_{\infty} \leq \alpha \rbrace.\]For example, let $n = 2, p = 2$ and
\[A^{T} = \begin{pmatrix} a_{11} & a_{21}\\ a_{12} & a_{22} \end{pmatrix}.\]Then,
\[\begin{equation}\nonumber C = \lbrace -\alpha \leq a_{11} p_{1} + a_{12} p_{2} \leq \alpha \rbrace \cap \lbrace -\alpha \leq a_{21} p_{1} + a_{22} p_{2} \leq \alpha \rbrace \end{equation}\]and
\[D = \lbrace -\alpha \leq d_{1} \leq \alpha \rbrace \cap \lbrace -\alpha \leq d_{2} \leq \alpha \rbrace.\]This is illustrated in Figure 2.
Solution of the primal problem
From the optimality condition of the dual problem, we can infer the primal solution given the assumption of the existence of $A^{-1}$.
During the formulation of the dual problem, we introduced the dummy variable $z = Ax$ and derived the stationary condition $z = y - p^{*}$. This implies that every solution $x^{*}$ of \eqref{eq:primal-problem} should satisfy”
\[A x^{*} = y - p^{*}\]where $p^{*}$ is a solution of the dual problem \eqref{eq:dual-problem}. Therefore, if $A^{-1}$ exists, the solution is:
\[x^{*} = A^{-1} \left( y - P_{C}(y) \right).\]Since $P_{C}$ is a projection onto a convex set $C$, it follows that $x^{*}$ is also nonexpansive mapping as a function of $y$. This is not obvious and would probably be hard to show without the dual formulation.
The nonexpansive property:
\[\norm{P_{C}(y) - P_{C}(\tilde{y})} \leq \norm{y - \tilde{y}}.\]is demonstrated in Figure 3A. For constrast, the projection onto a non-convex set $N$ is depiced in Figure 3B.
References
- Tibshirani, R. (1996). Regression Shrinkage and Selection Via the Lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267–288. https://doi.org/https://doi.org/10.1111/j.2517-6161.1996.tb02080.x
- Tikhonov, A. N., & Arsenin, V. Y. (1977). Solutions of ill-posed problems (p. xiii+258). V. H. Winston \& Sons. https://catalogue.nla.gov.au/catalog/720231
- Boyd, S., & Vandenberghe, L. (2008). Subgradients Notes. https://see.stanford.edu/materials/lsocoee364b/01-subgradients_notes.pdf