The purpose of this tutorial is to give a friendly introduction on how to use the persistent homology that does not require substantial knowledge of topological methods. To illustrate the use of persistent homology in machine learning we apply it to the MNIST data set of handwritten digits. A very similar approach can be applied to any point cloud data and can be generalized to higher dimensions.
A pure topological classification cannot distinguish between individual numbers, as the numbers are topologically too similar. For example, numbers 6 and 9 are topologically the same if we use this style for writing numbers. Persistent homology, however, gives us more information. The process is described as follows and illustrated in Figure 1. Define a filtration on the vertices of the graph corresponding to the image pixels, adding vertices and edges as we sweep across the image (Figure 1A,B). This adds spatial information to the topological features. For example, though 6 and 9 both have a single loop, it will appear at different locations in the filtration. Then, compute the persistent homology given the simplex stream from the filtration to get the finite set of intervals called Betti barcodes (Figure 1C).
Finally, extract 4 features from the k-dimensional barcode from the invariants discussed in (Adcock et al., 2013). For each of 4 sweep directions: top, bottom, right, left and dimensions: 0 and 1, compute 4 features. This gives a total of 32 features per image. On the extracted features from a set of images, we then apply a support vector machine (SVM) learning algorithm to classify the images.
This blog post starts by a short introduction to Topological Data Analysis and Computational Topology. Next, the extraction of topological features is explained. Finally, the empirical classification results on a subset of the MNIST database are presented including the evaluation.
The aim is to demonstrate the classification potential of the technique and not to outperform the existing models. For a more interesting example of using this technique on a clinical data set to classify hepatic lesions, see (Adcock et al., 2013).
All scripts are available on GitHub repository including a processed version of the dataset. Also, freely available computational topology package Dionysus 2 is used for the computation of persistent homology.
Table of contents
- Introduction
- Terminology
- Extracting the graph structure
- Extracting the topological features
- Empirical results
- Source code
- References
Introduction
Persistent homology is a fascinating mathematical tool that continues to be studied, developed, and applied. Topology applied to real-world data sets using persistent homology has begun to look for applications in machine learning, including deep learning (Brüel-Gabrielsson et al., 2020). Topology is mainly used in a pre-processing step to provide robust features for learning. The developed topological techniques, mostly deal with point clouds, i.e. finite sets of data points in space. Point clouds are typically captured by a variety of imaging devices, such as MRI or CT scanners. With the greater availability of such devices, this type of data is being generated at an increasing rate. Our data is often a finite set of noisy samples from some underlying space. The data sets are often very noisy and contain a lot of missing information, especially biological data sets. Our ability to analyze this data, both in terms of the amount and the nature of the data, is getting out of step with the data we generate (Carlsson, 2009). Topology can be used to make a useful contribution to the analysis of such data sets and it is especially helpful in studying them qualitatively.
The problem we are trying to solve in this tutorial is how to extract the topological features that can be used as an input to standard machine learning algorithms. We will use a similar approach as described in (Adcock et al., 2013). From each image, we first construct a graph, where pixels of the image correspond to vertices of the graph and we add edges between adjacent pixels (Figure 2A,B). We then extract 0- and 1-dimensional topological features called Betti numbers denoted by $\beta_{0}$ and $\beta_{1}$. For example, a torus has one connected component giving $\beta_{0} = 1$, and two cycles or loops, giving $\beta_{1} = 2$ (Figure 2C).
Terminology
- Topology is a branch of mathematics that deals with qualitative geometric information. This includes the classification of loops and higher-dimensional surfaces.
- Topological data analysis and computational topology deal with the study of topology using a computer.
- Persistent homology is an algebraic method for discerning topological features of data.
- Connected component (or connected cluster of points) is a 0-dimensional feature and cycle (or loop) is a 1-dimensional feature.
- Simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts.
- Filtration is the sequence of simplicial complexes, with an inclusion map from each simplicial complex to the next.
- Barcode is a visual representation of the persistence of the topological features. Longer bars represent significant features of the data. Shorter bars are due to irregularities or noise.
Extracting the graph structure
The pre-processing steps to expose the topology of the digits, shown in the image of a handwritten digit 8 in Figure 3, are as follows.
- Load the MNIST image of a handwritten digit.
- Produce a binary image by thresholding.
- Reduce the image to a skeleton of 1-pixel width using the popular Zhang-Suen thinning algorithm.
- Construct a graph $G$ from the skeleton.
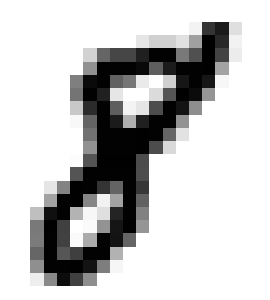
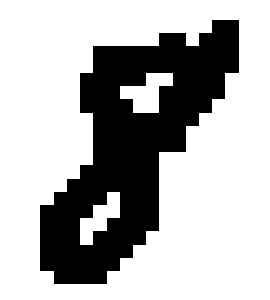
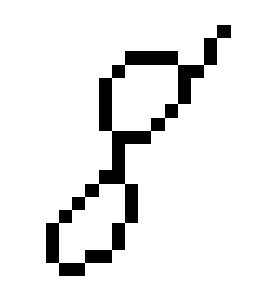
To construct the graph $G$ from the 1-pixel width skeleton, we treat the pixels of the skeleton as vertices of $G$ and add the edges between adjacent vertices and then remove all created cycles of length 3. Intuitively, we connect the points while trying not to create new topological features. The result for the image of a handwritten digit 8 is a graph in Figure 3. The resulting graph in this example consists of one connected component with two cycles, so no new topological features were added.
Extracting the topological features
Construct a simplex stream for computing the persistent homology using the following filtration on the graph $G$ embedded in the plane. Sweep across the plane while adding the vertices and edges of graph $G$. From the simplex stream, compute the persistent homology to get the Betti barcodes. The Dionysus 2 package can be used for the computation of persistent homology. See the package documentation (Morozov, Accessed on Sep 25, 2020) for details.
Figure 4 shows the result of this technique applied on the image of a handwritten digit 8. In this example, we sweep across the plane to the top in a vertical direction $y \in (-\infty, \infty)$.
Betti 0 barcode $\beta_{0}$ consists of one interval $[2, \infty)$, which clearly shows the single connected component with the birth time of 2 when the first vertex of $G$ is added.
Betti 1 barcode $\beta_{1}$ consists of two intervals $[10, \infty)$ and $[18, \infty)$, with birth times of 10 and 18 corresponding to the births of the two cycles. The birth of the cycle is the value of $y$ when the loop closes in the embedded graph $G$ as we sweep to the top.
Finally, extract the following features from each of the k-dimensional Betti barcodes in the following way. Denote the endpoints of Betti barcode intervals with:
\[x_{1}, y_{1}, ..., x_{n}, y_{n}\]where $x_{i}$ represents the beginning and $y_{i}$ the end of each interval. From the endpoints compute 4 features from the invariants discussed in (Adcock et al., 2013) that take into account all of the bars lengths and endpoints:
\[\begin{align*} f_{1}&=\sum_{i} x_{i} (y_{i} - x_{i}) \\ f_{2}&=\sum_{i} (y_{\max} - y_{i})(y_{i} - x_{i}) \\ f_{3}&=\sum_{i} (y_{\max} - y_{i})^{2} (y_{i} - x_{i})^{4} \\ f_{4}&=\sum_{i} x_{i}^{2} (y_{i} - x_{i})^{4} \\ \end{align*}\]For each of the 4 sweep directions: top, bottom, right, left and for each $k$-dimensional Betti barcode, $k = 0, 1$, we compute the defined 4 features $f_{1}, \dots, f_{4}$. This gives us a total of $4 \cdot 2 \cdot 4 = 32$ features per image.
Empirical results
Data set consisted of extracted topological features of 10000 images of handwritten digits from MNIST database. Data set was split 50:50 in train and test set so that each had 5000 examples. SVM with RBF kernel was used for classification of the images based on the extracted topological features. The empirical classification results are as follows. Accuracy on the train set using 10-fold cross-validation was $0.88 (\pm 0.05)$. Accuracy on the test set was 0.89.
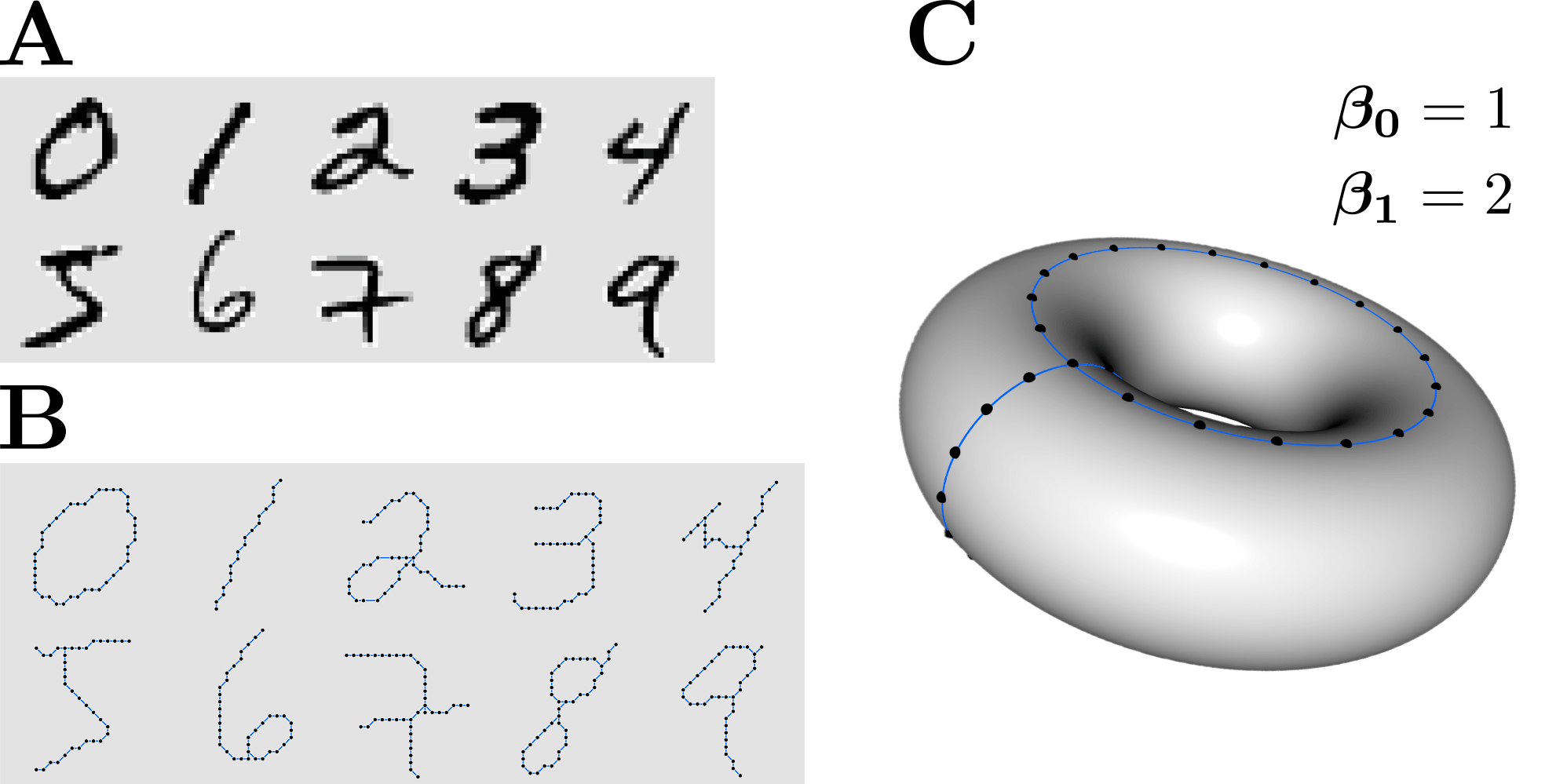
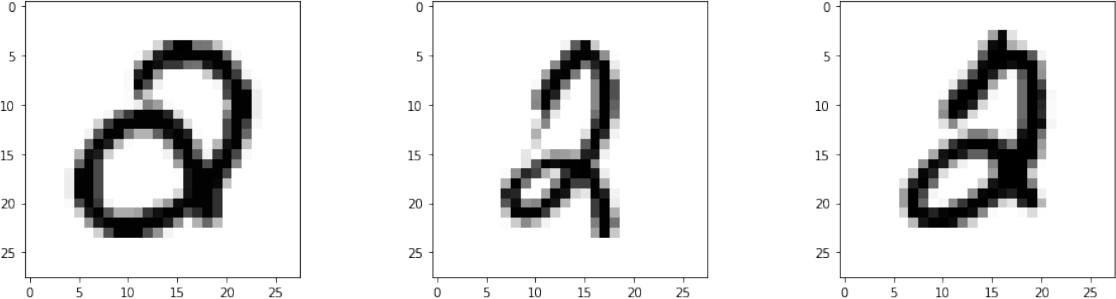
We now examine the common misclassifications. There were only 3 examples of the number 2 being mistaken for number 0, they are shown in Figure 5. The reason is that the number 2 was written with a loop that appears in the region that is close to the loop in number 0.
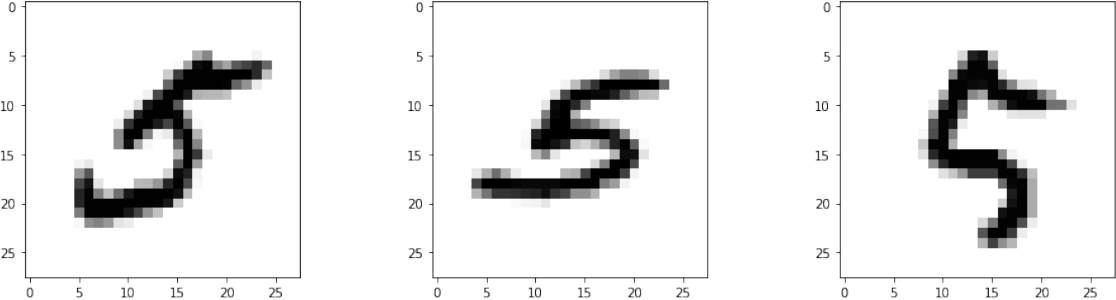
For number 5 we got the lowest F1 score of 0.75. It was misclassified as number 2 in 32 examples in the test set. The first three examples are shown in Figure 6. This was expected since these two numbers are topologically the same with no topological features (e.g. loops) appearing in different regions.
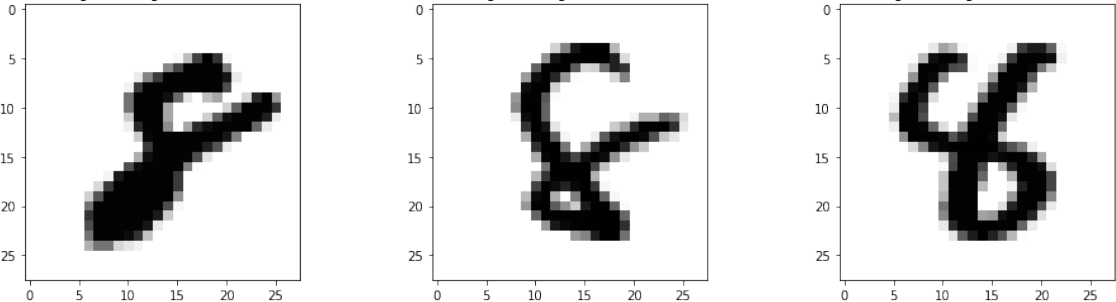
Number 8 was misclassified as number 4 in 21 examples from the test set. The first three examples are shown in Figure 7. We see the stylistic problems that caused the misclassifications. The top loop of number 8 was not closed which made it topologically more similar to number 4 written with a loop.
Source code
The repository containing all Python scripts for this tutorial including the processed version of the data set is available here:
References
- Adcock, A., Carlsson, E., & Carlsson, G. (2013). The Ring of Algebraic Functions on Persistence Bar Codes. https://arxiv.org/abs/1304.0530
- Brüel-Gabrielsson, R., Nelson, B. J., Dwaraknath, A., Skraba, P., Guibas, L. J., & Carlsson, G. (2020). A Topology Layer for Machine Learning. https://arxiv.org/abs/1905.12200
- Carlsson, G. E. (2009). Topology and data. Bulletin of the American Mathematical Society, 46, 255–308. https://api.semanticscholar.org/CorpusID:1472609
- Morozov, D. (Accessed on Sep 25, 2020). Dionysus 2 documentation. https://mrzv.org/software/dionysus2/